54. 螺旋矩阵
题意:
给定一个 m 行 n 列 二维矩阵,输出矩阵元素按顺时针螺旋顺序访问的结果
思路:
简单类似机器人寻路算法遍历即可
遍历后直接在原地修改值为非法值,停止条件可以设为当已寻路长度达到矩阵内元素数量即可
反思:
小错误太多:语法错误(将 int[] 赋给 int 等),边界条件不清晰(nx > -1 而不是 nx > 0),寻路成功后没有移动(用 nx 探路成功后应将 nx 赋给 tx 来移动)
时刻注意,while 循环和 for 循环的区别就是 while 循环不会自己进行步进过程,不要忘记了自己加上步进操作
public class Solution {
private int[] dx = {1,0,-1,0};
private int[] dy = {0,1,0,-1};
public List<Integer> spiralOrder(int[][] matrix) {
List<Integer> ans = new LinkedList<>();
if (matrix.length == 0)
return ans;
int m = matrix.length, n = matrix[0].length;
int tx = -1,ty = 0;
int dir = 0;
while (ans.size() < m*n) {
int nx = tx + dx[dir], ny = ty + dy[dir];
if (nx > -1 && nx < n && ny > -1 && ny < m && matrix[ny][nx] > -100) {
ans.add(matrix[ny][nx]);
matrix[ny][nx] = -101;
tx = nx;
ty = ny;
} else {
dir = (dir + 1) % 4;
}
}
return ans;
}
}240. 搜索二维矩阵 II
题意:
编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性:
每行的元素从左到右升序排列。
每列的元素从上到下升序排列。

思路:
研究矩阵的右上角元素可发现:该元素(15)满足【比自己小的元素都在自己左方,比自己大的元素都在自己下方】,同时对于其他任意位置元素也满足同样的性质(类似于 二叉搜索树 的结构),这样可以保证在O(m+n) 内完成搜索过程。
class Solution {
public boolean findNumberIn2DArray(int[][] matrix, int target) {
int m = matrix.length;
if (m == 0) return false;
int n = matrix[0].length;
int tx = n-1,ty = 0;
boolean flag = false;
while (tx >= 0 && tx < n && ty >= 0 && ty < m) {
int num = matrix[ty][tx];
if (num == target) {
flag = true;
break;
} else if (num < target) {
ty++;
} else {
tx--;
}
}
return flag;
}
}59. 螺旋矩阵 II
题意:
给你一个正整数 n ,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。
思路:
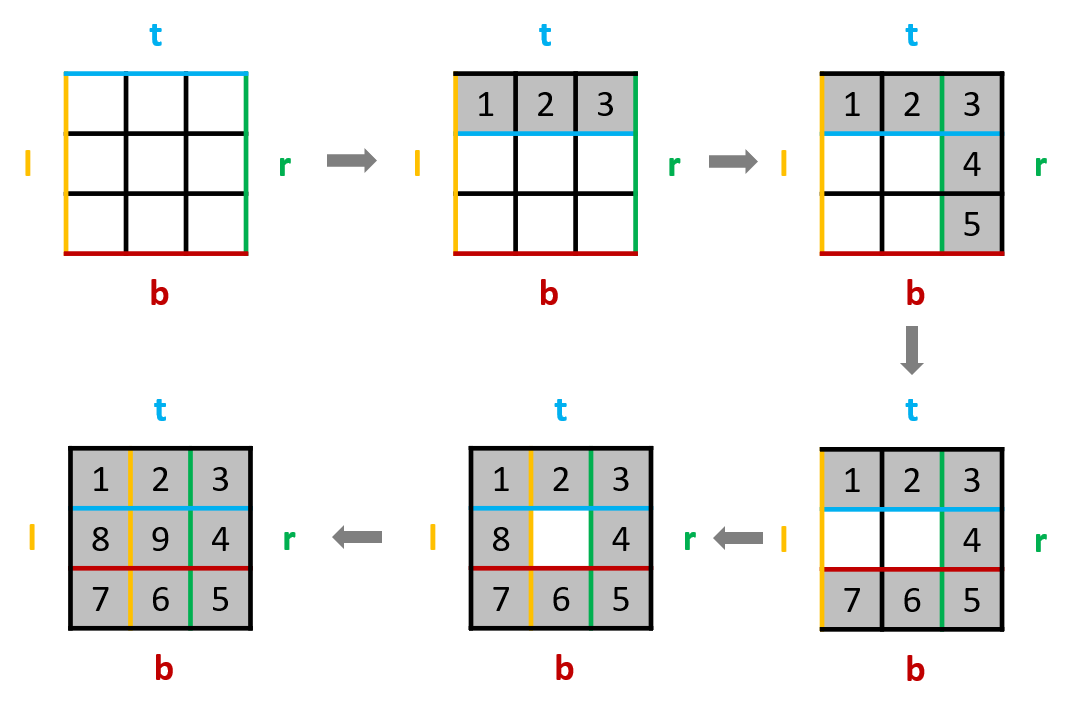
题目的基本思路和 54. 螺旋矩阵 是基本类似的,这里提供了一种和机器人寻路法不同的方法:观察到每次进行单方向移动时都是相对于上次同一方向移动的距离逐渐缩短,可以考虑采用设置四边界,并且在一方向移动完之后缩短对应的边界(来自作者:jyd 的题解)
class Solution {
public int[][] generateMatrix(int n) {
int l = 0, r = n - 1, t = 0, b = n - 1;
int[][] mat = new int[n][n];
int num = 1, tar = n * n;
while(num <= tar){
for(int i = l; i <= r; i++) mat[t][i] = num++; // left to right.
t++; //缩短上边界
for(int i = t; i <= b; i++) mat[i][r] = num++; // top to bottom.
r--; //缩短右边界
for(int i = r; i >= l; i--) mat[b][i] = num++; // right to left.
b--; //缩短底边界
for(int i = b; i >= t; i--) mat[i][l] = num++; // bottom to top.
l++; //缩短左边界
}
return mat;
}
}115. 不同的子序列
J 25. 合并两个排序的链表
题意:
输入两个递增排序的链表,合并这两个链表并使新链表中的节点仍然是递增排序的。
思路:
使用三个指针进行移动(目标指针,L1,L2)
对L1,L2平行移动比较,比较完成之后指针直接指向目标的节点,然后让那个节点往后移动,然后再进行下一步比较,不需要另外再 new node
class Solution {
public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
ListNode head = new ListNode(0);
ListNode curr = head;
while (l1 != null && l2 != null) {
if (l2.val > l1.val) {
curr.next = l1;
l1 = l1.next;
curr = curr.next;
} else {
curr.next = l2;
l2 = l2.next;
curr = curr.next;
}
}
if (l1 != null) curr.next = l1;
if (l2 != null) curr.next = l2;
return head.next;
}
// 另一种递归做法
public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
if(l1 == null || l2 == null)
return l1 == null ? l2 : l1;
if(l1.val<l2.val)
{
l1.next = mergeTwoLists(l1.next, l2);
return l1;
}
else
{
l2.next = mergeTwoLists(l1, l2.next);
return l2;
}
}
}25. K 个一组翻转链表
题意:
k个一组翻转链表,当最后一组不满k个时不翻转
思路:
递归:将链表每个需要翻转的一组视作一个整体,每个整体代表一次递归过程
// 当 k == 2时
class Solution {
public ListNode swapPairs(ListNode head) {
return next(head);
}
ListNode next(ListNode start) {
if (start == null || start.next == null) {
return start;
} else {
// 对于每一组的前后两个节点,先让前节点next指向下一组结果,然后再将后节点next改为前节点
// 返回后节点即为该组的代表结果
ListNode after = start.next;
start.next = next(after.next);
after.next = start;
return after;
}
}
}
// 通用情况
class Solution {
public ListNode reverseKGroup(ListNode head, int k) {
// 每个递归是本区域的头部节点
if (head == null || k < 2) return head;
ListNode cur = head;
int count = 1;
// 遍历到区域尾,这个尾部将会变成区域头部返回
while (cur != null && count < k) {
count++;
cur = cur.next;
}
// 如果到了末尾直接返回头部
if(cur == null) return head;
// 下一个区域的头部
ListNode other = cur.next;
// 注意区域第一个节点(最后将被移动到最后)的next应该指向下一个区域的头节点
ListNode prev = reverseKGroup(other, k);
// temp从head开始,通过 temp next prev 三个指针进行区域内翻转,方式和 J24 反转链表相同
ListNode temp = head;
ListNode next;
// 直到temp和下一个区域重合前
while (temp != other) {
next = temp.next;
temp.next = prev;
prev = temp;
temp = next;
}
return cur;
}
}28. 实现 strStr()
题意:
实现 strStr() 函数。
给定一个 haystack 字符串和一个 needle 字符串,在 haystack 字符串中找出 needle 字符串出现的第一个位置 (从0开始)。如果不存在,则返回 -1。
思路:
使用 KMP(Knuth-Morris-Pratt)算法
核心思想是通过另一个等长度数组维护原字符串的最长公共前缀和后缀信息,称为 LPS
LPS[i] 记录的信息是:字符串从头开始到 i 位置的这段字符串公共前后缀(前缀=后缀)的最大长度。比如(ABCDABD)的LPS数组为{0, 0, 0, 1, 2, 0},LPS[5] = 2 代表 ABCDAB 的公共前后缀为 2
在LPS 已知的情况下,我们在匹配一个字串失败时,可以不用再回退到原位置 + 1的位置,而是可以直接根据前后缀相同,只回退到当前相同的位置即可

class Solution {
public int strStr(String haystack, String needle) {
int n = haystack.length();
int m = needle.length();
if (m == 0) {
return 0;
}
int i = 0,j = 0;
int[] lps = getLPS(needle);
while(i < n) {
// 匹配时共同增加
if (haystack.charAt(i) == needle.charAt(j)) {
i++;j++;
// 如果 needle 串匹配完成
if (j == m) {
// 返回子串在原串的起始位置
return i - m;
}
} else if (j > 0){
// 如果不匹配并且 j 匹配到一半,根据 lps 将 j 指针回退
j = lps[j - 1];
} else {
// 如果从起始位置就不匹配,移动 i 指针
i++;
}
}
return -1;
}
// LPS构造
int[] getLPS(String str) {
int[] lps = new int[str.length()];
// i 为检索指针,len 为当前字符串最大前缀位置
int i = 1,len = 0;
while (i < str.length()) {
// 若 i 指针能够延续前缀和后缀,那么更新 lps 值为 len+1
if (str.charAt(i) == str.charAt(len)) {
lps[i++] = ++len;
} else if (len > 0) {
// 否则,判断 len 是否大于 0;
// 大于 0 时,将len退回到上一处前缀相同的位置进行匹配
len = lps[len - 1];
} else {
// len为0,无法再往前比较
i++;
}
}
return lps;
}
}190. 颠倒二进制位
题意:
颠倒给定的 32 位无符号整数的二进制位。
思路:
- 逐位颠倒
依次移动位置并将结果放到新结果中
- 分治
将颠倒操作分治到各个子部分进行,最后一级操作会变成交换所有奇偶位
// 逐位颠倒
public class Solution {
public int reverseBits(int n) {
int rev = 0;
for (int i = 0; i < 32 && n != 0; ++i) {
rev |= (n & 1) << (31 - i);
n >>>= 1;
}
return rev;
}
}
// 位运算分治
public class Solution {
private static final int M1 = 0x55555555; // 01010101010101010101010101010101
private static final int M2 = 0x33333333; // 00110011001100110011001100110011
private static final int M4 = 0x0f0f0f0f; // 00001111000011110000111100001111
private static final int M8 = 0x00ff00ff; // 00000000111111110000000011111111
public int reverseBits(int n) {
n = n >>> 1 & M1 | (n & M1) << 1;
n = n >>> 2 & M2 | (n & M2) << 2;
n = n >>> 4 & M4 | (n & M4) << 4;
n = n >>> 8 & M8 | (n & M8) << 8;
return n >>> 16 | n << 16;
}
}23. 合并K个升序链表
题意:
合并 K 个升序链表
思路:
使用优先队列,将全部链表头推入这个队列,每次取出其最小值的node,然后再将node的下一位加入队列
class Solution {
public ListNode mergeKLists(ListNode[] lists) {
PriorityQueue<ListNode> queue = new PriorityQueue<>((a,b) -> a.val - b.val);
for (ListNode node: lists) {
if (node != null) {
queue.offer(node);
}
}
ListNode head = new ListNode(0);
ListNode tail = head;
while (!queue.isEmpty()) {
ListNode node = queue.poll();
tail.next = node;
tail = tail.next;
if (node.next != null) {
queue.offer(node.next);
}
}
return head.next;
}
}33. 搜索旋转排序数组
题意:
整数数组升序排列,保证没有重复值。现在将nums在某个下标上进行旋转,对于转换后的数组 nums 和整数 target,如果 nums 中存在这个目标值 target,则返回其下标,否则返回 -1
思路:
带条件的二分查找,根据 mid 值不同,分为 left 和 mid 形成有序数组(mid > left)或者 right 和 mid 形成有序数组(right > mid)两种情况。不同情况下,根据 target 值所处的位置(大小)不同,向不同方向移动进行查找
class Solution {
public:
int search(vector<int>& nums, int target) {
int n = (int)nums.size();
if (!n) {
return -1;
}
if (n == 1) {
return nums[0] == target ? 0 : -1;
}
int l = 0, r = n - 1;
while (l <= r) {
int mid = (l + r) / 2;
if (nums[mid] == target) return mid;
// left -> mid 形成有序数组
if (nums[0] <= nums[mid]) {
// target 位于 left <-> mid 之间,向左缩进
if (nums[0] <= target && target < nums[mid]) {
r = mid - 1;
} else { // target 在 left <-> mid 之外,向右缩进
l = mid + 1;
}
} else { // mid -> right 形成有序数组
if (nums[mid] < target && target <= nums[n-1]) {
l = mid + 1;
} else {
r = mid - 1;
}
}
}
return -1;
}
}81. 搜索旋转排序数组 II
题意:
相比 33.搜索旋转排序数组 多出了重复元素的情况,二分查找时可能存在 a[l] = a[mid] = a[r],此时无法简单判断区间 [l,mid] 和 区间 [mid+1,r] 的有序性,这种情况下只能步进缩减区间
解法:
class Solution {
public:
int search(vector<int>& nums, int target) {
int n = (int)nums.size();
if (!n) {
return -1;
}
if (n == 1) {
return nums[0] == target ? 0 : -1;
}
int l = 0, r = n - 1;
while (l <= r) {
int mid = (l + r) / 2;
if (nums[mid] == target) return true;
// 对于三点相同元素的极端情况
if (nums[l] == nums[mid] && nums[mid] == nums[r]) {
++l;
--r;
}
// left -> mid 形成有序数组
else if (nums[l] <= nums[mid]) {
// target 位于 left <-> mid 之间,向左缩进
if (nums[l] <= target && target < nums[mid]) {
r = mid - 1;
} else { // target 在 left <-> mid 之外,向右缩进
l = mid + 1;
}
} else { // mid -> right 形成有序数组
if (nums[mid] < target && target <= nums[r]) {
l = mid + 1;
} else {
r = mid - 1;
}
}
}
return false;
}
}153. 寻找旋转排序数组中的最小值
题意:
升序长度n的旋转数组找最小值
数组元素不重复,但是也有可能没发生旋转
解法:
二分
本身不难,但是注意边界情况
class Solution {
public:
int findMin(vector<int>& nums) {
int n = (int)nums.size();
if (n == 1)
return nums[0];
int l = 0, r = n-1;
int mid;
while(l < r) {
mid = (l+r)/2;
if (nums[l] > nums[r] && nums[mid] >= nums[l]) {
l = mid+1;
} else {
r = mid;
}
}
return nums[l];
}
};264. 丑数 II
题意:
给你一个整数 n ,请你找出并返回第 n 个 丑数 。
解法:
要求我们返回仅包含2,3或5的正整数,并且需要(按顺序)数到第n个这样的数,那么核心思想就是从2 3 5的倍数开始逐个数数,一直数到第n个丑数
class Solution {
public:
int nthUglyNumber(int n) {
vector<int> dp(n + 1);
dp[1] = 1;
// 建立三个指针,表示【下一个丑数】是当前指针指向的丑数乘以对应的质因数
int p2 = 1, p3 = 1, p5 = 1;
for (int i = 2; i <= n; i++) {
int num2 = dp[p2] * 2, num3 = dp[p3] * 3, num5 = dp[p5] * 5;
// 选取这三个指针对应的丑数中最小的那个,并且增加相应的指针
dp[i] = min(min(num2,num3),num5);
if (dp[i] == num2) {
p2++;
}
if (dp[i] == num3) {
p3++;
}
if (dp[i] == num5) {
p5++;
}
}
return dp[n];
}
};208. 实现 Trie (前缀树)
题意:
实现一个前缀树,完成插入,查找词组,查找前缀等操作
解法:
class Trie {
boolean isEnd;
Trie[] children;
public Trie() {
isEnd = false;
children = new Trie[26];
}
public void insert(String word) {
if(word.equals("")) {
isEnd = true;
} else {
int i = word.charAt(0) - 'a';
Trie trie;
// 如果children已经包含这个字符,那么直接使用即可
// 否则可能导致原本存放的前缀被覆盖
if(children[i] == null) {
trie = new Trie();
children[i] = trie;
} else {
trie = children[i];
}
trie.insert(word.substring(1));
}
}
public boolean search(String word) {
if (word.equals("")) return this.isEnd;
int i = word.charAt(0) - 'a';
return children[i] != null && children[i].search(word.substring(1));
}
public boolean startsWith(String prefix) {
if(prefix.equals("")) return true;
int i = prefix.charAt(0) - 'a';
return children[i] != null && children[i].startsWith(prefix.substring(1));
}
}213. 打家劫舍 II
题意:
在原本打家劫舍问题(不能偷窃相邻房屋)的基础上,添加了“第一个房屋和最后一个房屋永远相连”的限制
解法:
仍然需要动态规划,但是由于新加入的限制,dp[0] 和 dp[n] 的结果出现关联,无法简单使用之前的区间递推方式
除了考虑新的dp方法之外,由于限制仅仅发生在头尾两个元素之前,可以考虑“拆解限制以满足原本的规律的dp递推情况”
由于第一个房子和最后一个房子的选择必然对立,那么可以考虑将这两个元素拆出:如果保证不选择最后一个房间,那么可选下标范围是:[0,length-2];如果保证不选择第一个房间,那么可选下标范围是:[1,length-1];在这个范围内,我们可以按照原本的递推式进行计算:dp[i]=max(dp[i−2]+nums[i],dp[i−1])
另外,根据屋最该总金额只和该房屋前两间房屋的最高总金额相关,那么可以考虑使用滚动数组代替dp数组:每个时刻只需要存储前两间房屋的最高总金额
class Solution {
public:
int rob(vector<int>& nums) {
int length = nums.size();
if (length == 1) {
return nums[0];
} else if (length == 2) {
return max(nums[0], nums[1]);
}
// 拆分首尾发生的冲突,在两种对立情况下取最大值
return max(robRange(nums, 0, length - 2), robRange(nums,1,length-1));
}
int robRange(vector<int>& nums, int start, int end) {
// 使用滚动数组代替dp数组
int first = nums[start], second = max(nums[start], nums[start+1]);
for (int i = start + 2; i <= end; i++) {
int temp = second;
second = max(first + nums[i],second);
first = temp;
}
return second;
}
};403. 青蛙过河
21/4/29
题意:
一只青蛙想要过河。 假定河流被等分为若干个单元格,并且在每一个单元格内都有可能放有一块石子(也有可能没有)。 青蛙可以跳上石子,但是不可以跳入水中。
给你石子的位置列表 stones(用单元格序号 升序 表示), 请判定青蛙能否成功过河(即能否在最后一步跳至最后一块石子上)。
开始时, 青蛙默认已站在第一块石子上,并可以假定它第一步只能跳跃一个单位(即只能从单元格 1 跳至单元格 2 )。
如果青蛙上一步跳跃了 k 个单位,那么它接下来的跳跃距离只能选择为 k - 1、k 或 k + 1 个单位。 另请注意,青蛙只能向前方(终点的方向)跳跃。
思路:
DFS:
不考虑优化的情况下,明显可以使用深度优先搜索,即按照某个跳跃方式不断向前搜索直到遍历完所有结果,当不满足条件时再回退,然而该情况下复杂度将会升到指数级
优化点1:记忆化搜索。由于当前可以选择的跳跃距离受上次跳跃距离影响,仅需记录「现在所处的石子编号」以及「上一次跳跃距离」两个变量即可
优化点2:下个石头位置的查找。搜索某个位置的某个跳跃长度是否存在石子时,可以将原数组反向记录一个<距离,下标>的map,减少搜索消耗
dp:
和上面的分析结果一致,容易得出dp[i][j]的定义为「现在所处的石子编号」「上一次跳跃距离」时青蛙的可达性
容易得出状态转移方程为:dp[i][k]= dp[j][k-1] || dp[j][k] || dp[j][k+1] ,j为上次所在的石子编号,满足 stone[i]-stone[j] = k
代码:
// dfs解法
class Solution {
public:
vector<unordered_map<int, int>> rec;
// 对可行的跳跃结果的深度优先搜索
bool dfs(vector<int>& stones, int i, int lastDis) {
// 如果已经搜索到了最后一个石子,返回true
if (i == stones.size() - 1) {
return true;
}
// 如果已经记忆过了【位于第 i 个石子,上次跳跃距离为 lastDis 情况下】的可达性结果,直接返回
if (rec[i].count(lastDis)) {
return rec[i][lastDis];
}
// 开始根据当前位置和 lastDis,搜索本次跳跃距离为 curDis = [lastDis-1,lastDis+1]间的每个情况的结果
for (int curDis = lastDis - 1; curDis <= lastDis + 1; curDis++) {
if (curDis > 0) {
// 下次跳跃累计距离为 curDis + stones[i] ,在stones数组中搜索这个结果
int j = lower_bound(stones.begin(), stones.end(), curDis + stones[i]) - stones.begin();
if (j != stones.size() && stones[j] == curDis + stones[i] && dfs(stones, j, curDis)) {
// 如果存在,且递归搜索的结果也可达,那么该方案(rec[i][lastDis])可达
return rec[i][lastDis] = true;
}
}
}
return rec[i][lastDis] = false;
}
bool canCross(vector<int>& stones) {
int n = stones.size();
rec.resize(n);
return dfs(stones, 0, 0);
}
};